En introduisant les valeurs, sans effectuer les fractions, il vient en valeur absolue:

1/(O₂O'₁₎ = 7,5 . Ce qui fait O₂O'₁ = 13,3 cm. Calculons le grandissement :

|g₂| = O₂O'₁/O₂O₁ . Ce qui donne 1/3 .

La distance O₁F₂ vaut +30cm, et O₁F₁= - 5cm . La formule de conjugaison donne la distance objet 1/O₁A = - 20 + 3,33 = - 16,67 m^-1

algébriquement : O₁A = - 6,0cm

 

d) pour cette question, cliquez car ici, il n'y a plus de place !

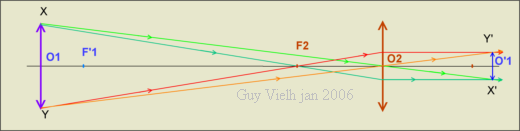
Construction du cercle oculaire.

L'image de la lentille objectif est trois fois plus petite : 2/3 = 0,67 cm.

Que d'efforts inutiles (sauf pour montrer que vous savez utiliser les formules et le grandissement ce qui est peut-être l'intention cachée du problème).

c) Pour que l'image vue par l'oeil se forme à l'infini, il est indispensable que l'image réelle de l'objet donnée par L1 (objectif) se forme au foyer objet de L2 c'est à dire en F2.

a) Le cercle oculaire est l'image du diaphragme de l'objectif donnée par l'oculaire .

Construire 2 rayons partant des extrémités de l'objectif : ceux passant par le foyer objet de l'oculaire et ceux traversant l'oculaire par son centre optique. Le cercle oculaire est X'Y'.

b) On n'a pas besoin de la formule de conjugaison pour avoir le diamètre du cercle oculaire. Thalès suffit : XY/O₁F₂ = X'Y'/O₂F₂ . (ben oui, après l'oculaire, les deux rayons parallèles à l'axe optique sont écartés de X'Y')

X'Y' = 2 . 10/30 = 0,67 cm

Mais comme l'énoncé le demande, faisons docilement le calcul du cercle oculaire en utilisant la formule de conjugaison: elle nous permet ce calculer la distance image de la deuxième lentille. La première lentille est l'objet. Appelons O'₁ l'image de O₁ formée par L₂.

 

7 : Construction du CERCLE OCULAIRE