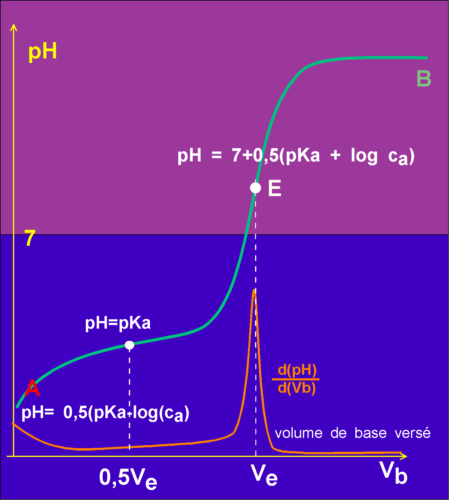
Alors [BH] est très proche de Ca. Donc Ka = [H+]²/Ca (point A sur le graphique: pH = 0,5(pKa - log Ca))
Si on ne peut pas négliger la dissociation (acide presque fort pKa <2)
Ka = [H+]²/(Ca - [H+]) ce qui conduit à résoudre l'équation du second degré:
Ka.Ca - [H+].Ka - [H+]² = 0
À la demi neutralisation [B-] = [BH] et par conséquent:
pH = pKa (d'après l'équation 1 )
A la neutralisation (point E), l'équation 3 devient: [B-] + [OH-] = [H+] + [Na+] en négligeant [H+] devant [OH-]
[B-] = Ca - [OH-] et [BH] = [OH-]
Ka = Ca . [H+]/ [OH-] = Ca . [H+]²/Ke ou encore : [H+]² = Ka . Ke / Ca et
pH = pKe/2 + 0,5(pKa + log Ca)
avec pKe = 14 pour l'eau.

L'acide BH a une concentration Ca. Sa constante d'acidité Ka = [B-] . [H+] / [BH]
on écrit la conservation de la matière: .. . . . . Ca = [BH] + [B-] (équation 2).
On rajoute la base concentrée de manière à ne pas faire varier le volume: Ca garde sa valeur.
On écrit la neutralité de la solution (éq 3):
[B-] + [OH-] = [H+] + [Na+] La base est NaOH, et la loi d'action de masse.
Ke = [H+] . [OH-] (équation 4)
On a un joli système de 4 équations qui se
simplifie si on peut faire des approximations. Par exemple, il s'agit d'un acide: dans l'équation 3 on néglige [OH-] devant [H+] on a donc [B-] = [H+]. (! au point A on n'a pas encore ajouté de soude : pas de Na+)
De plus, l'acide est faible cela veut dire que la majorité de l'espèce chimique BH n'est pas dissociée (si pKa >2 c'est bon).