
Portons (I) et (II) dans la formule de conjugaison : schéma sur fond jaune.
Si D-4.f est positif, il y a deux solutions .
Si D = 4.f une seule position reste c'est la situation "de Silbermann"
Si D < 4f : il n'y a pas de solution, pas d'image sur l'écran.
Comment obtenir f à partir des mesures de x? Nous appelons
d = x2-x1 donc d² = D² - 4f.D
d'où on tire
f = (D²-d²)/4D
dite formule de BESSEL.


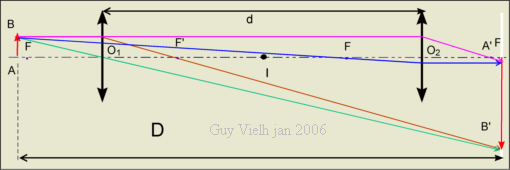
Entre un objet lumineux AB et l'écran blanc, on mesure une distance de D: AA' = D (algébriquement)
On dispose d'une lentille convergente de distance focale f . Si D est assez grand, il existe deux positions possibles pour que la lentille donne une image nette de AB sur l'écran.
Ces positions sont repérées sur le schéma par O1 et O2. On appelle "d" la distance O1O2.
Ces deux mesures permettent de trouver la distance focale f car il existe une relation entre D , d et f .
En utilisant I le milieu AA', on peut repérer les
distances qui figurent dans les relations de conjugaison en écrivant que IO = x (algébriquement) :
OA = OI + IA = - x - D/2 (I)
OA' = OA + D = D/2 + x (II) or![]()