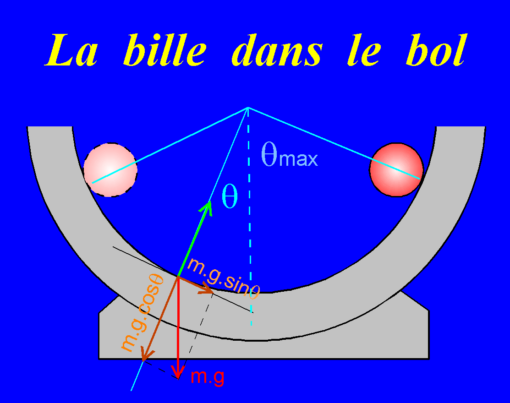
Si on peut négliger le fait que la bille roule, tout est exactement identique au pendule simple.
Le cas idéalisé est exactement le même que celui traité dans le pendule simple. Le traitement mathématique qui vient résoudre les équations donne naturellement les mêmes résultats:
q = qmax.cos(wot) et q' = -wo. qmax.sin(wot)
q" = -w²o. qmax.cos(wot) avec
w²o = g/r où r est le rayon de courbure du bol.
L'énergie se conserve ... Ce qui est intéressant c'est que la courbure du bol peut être autre chose qu'une portion de sphère.
Toutes les fantaisies sont permises. On établit l'équation différentielle et, quelquefois, on peut la résoudre analytiquement.
Avec un ordinateur et le programme adéquat, on peut toujours résoudre numériquement les équations.

Si on peut négliger le fait que la bille roule, tout est exactement identique au pendule simple.
Il y a une grande parenté avec le pendule simple ... Quoique !!!
Cela est vrai dans le cas où la bille est très petite. Sinon, elle roule et un mouvement propre de rotation s'ajoute au mouvement pendulaire du centre d'inertie. Le théorème du moment cinétique vient s'inviter à la fête et
cela complique le problème. On sait s'en sortir tout de même.
Quelquefois dans les problèmes on lit que la bille glisse sans frottement . On élimine ainsi la rotation de la bille autour de son centre géométrique. Le bol est une calotte sphérique.
Référentiel: laboratoire, habitation = terrestre = suffisamment galiléen.
Système étudié : la bille de masse "m"
Forces extérieures : le poids m.g (vertical vers le bas). réaction de la surface: sans frottement, perpendiculaire à la surface = centripète.