il vient donc : P.V = n.Na.k.T
Cela serait la loi du gaz parfait si
Na.k était égal à R , la constante du gaz parfait.
Voyons les valeurs de ces constantes:
La quantité de mouvement échangée est:
2 . m . vx . {S.vx.a/(2.V)} = F = P . S
m . vx . vx.a/V = P soit a. m. vx² = P.V
or m.vx² = 3.k.T et a = n.Na . En utilisant le théorème de Pythagore à 3 dimensions, on montre que vx² = <v²>/3
il vient donc : P.V = n.Na.k.T
Cela serait la loi du gaz parfait si
Na.k était égal à R , la constante du gaz parfait.
Voyons les valeurs de ces constantes:
Na = 6,022.1023 mol-1
k = 1,380.10-23 J.K-1
R = k.Na = 8,314
Ben voilà! La loi du gaz parfait résulte de la conservation de la quantité de mouvement dans les chocs et de la 3° loi de Newton.


Chaque molécule a une énergie cinétique
Ec= 0,5. m . vi².
L'énergie totale est la somme des énergies individuelles E = 0,5 . a.m .<v²>
où <v²> est la moyenne des carrés des vitesses
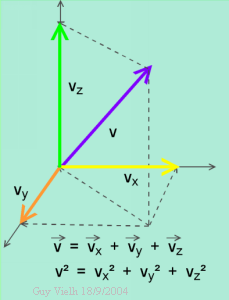
Le théorème de Pythagore dit que v² = vx² + vy² + vz²
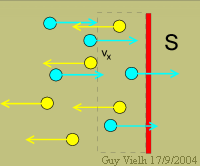
Nous nous intéressons à ce qui se passe sur l'axe Ox. Nous pouvons écrire la même chose pour les deux autres directions. Devant la surface S, combien de molécules vont frapper cette surface dans la seconde qui vient?
Toutes celles qui sont contenues dans le volume S . vx? La moitié seulement car les jaunes s'éloignent et ne frapperont pas.
Combien sont-elles dans le cadre pointillé? le volume dans le cadre pointillé est de S.vx
il contient S.vx.a/V molécules dont la moitié va frapper la surface S. soit : {S.vx.a/(2.V)}