
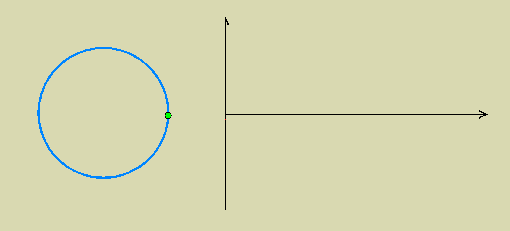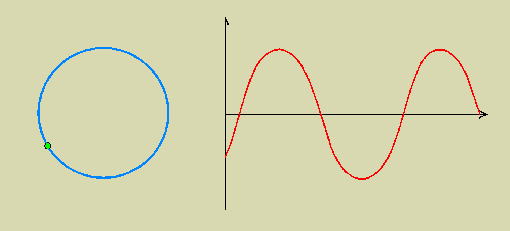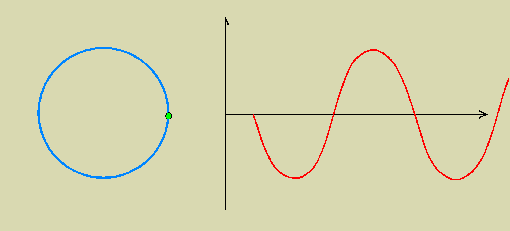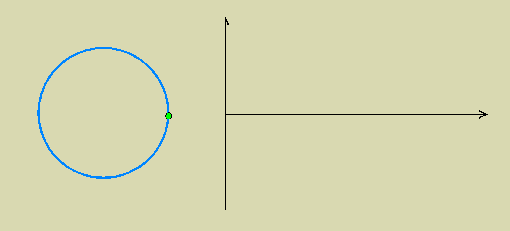
Tous les points M tels que x/c = k.T = k périodes (le point vert a juste le temps de faire k tours avant que le signal progressant arrive en x) ont le même mouvement.
Ils sont "EN PHASE".
Lorsque le signal est émis depuis un temps suffisant pour qu'il ait atteint tous les points
dont nous parlons, tous les points en phase montent et descendent en même temps.
La distance qui sépare deux points en phase consécutifs est parcourue par le signal en une période : cette distance est la longueur d'onde l.
l = c . T = c / f
Remarquez que, sur la deuxième illustration, l'onde , son arrêt et son début se propagent toujours à la même vitesse.


La projection du point vert (appartenant au cercle bleu tournant à vitesse constante) sur l'axe vertical est R.sin (2pft)
A droite, en rouge est porté la représentation graphique R.sin (2pft) en fonction du temps.
Comme sur l'écran de l'oscilloscope.
Ben oui, sur l'écran de l'oscilloscope, horizontalement le spot est entraîné par la "base de temps". L'abscisse est proportionnelle au temps ! (c'est du temps)
Pour un phénomène réel, la perturbation créée par le point vert se déplace dans la direction de la flèche noire (dans d'autres directions aussi
peut être mais nous ne nous en occupons pas) avec la célérité "c" de l'onde.
A la distance x1, le signal va mettre une durée x1/v pour venir depuis la source. Les événements qui se déroulent à l'abscisse x1 ressemblent beaucoup (à l'amplitude près) à ce qui est arrivé à la source mais avec un retard x1/c.