Il est facile de montrer que 0,5.m.g.r.q²max = Ec au point bas = Ep au point haut.
Faisons la somme de ces deux formes d'énergie: y'a un os. cos q avec q = qmax.cos(wot) est une voie très ardue ! En cherchant dans le formulaire des relations trigo nous trouvons : 1-cosq = 0,5 . sin² (q/2) et comme nous avons q petit 1-cosq = 0,5.q²
alors Ep = 0,5.m.g.r.q²max.cos²(wot)
portons la valeur w²o = g/r dans Ec
Ec = 0,5.m.(g/r). q²max.sin²(wot) Maintenant on peut additionner et
E = Ep + Ec = 0,5.m.g.r.q²max = constante ( dans le cas idéal sans frottement)
Il est facile de montrer que 0,5.m.g.r.q²max = Ec au point bas = Ep au point haut.
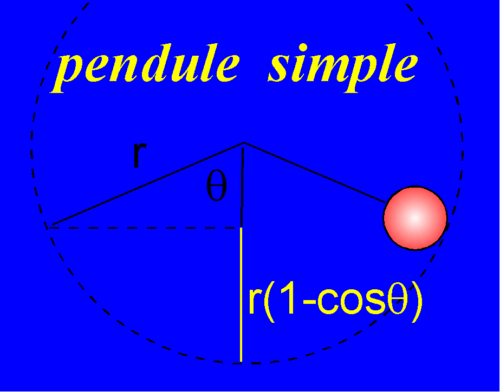
L'angle q a été fortement exagéré pour la lisibilité du schéma. Ce qu'on fait dans le pendule simple repose sur le fait que q est petit (<15°)
La fiche précédente nous a donné les équations du mouvement du pendule simple. La bille est réduite à un point circulant à la distance "r" du centre de rotation.
q = qmax.cos(wot) et q' = -wo. qmax.sin(wot) ; q" = -w²o. qmax.cos(wot) avec wo = g/r où r est la longueur de la ficelle.
Étant entendu qu'on lâche le pendule en son point haut en déclenchant le chronomètre.
L'énergie du pendule est répartie en deux "postes" :
Ecinétique = 0,5.m.v² = 0,5.m.(r.q')²
Epotentielle = m.g.z mais
z = zo + r.( 1- cos q ) rien ne nous empêche de choisir zo = 0 (altitude du point bas).
Ecinétique = 0,5.m.(wo)². (qmax.sin(wot))²
Epotentielle = m.g.r.( 1- cos q )
