en écrivant n2/1 = c1 / c2.
Cela nous fait: sin(i) = n2/1 . sin (r)
Ben voilà, la relation de Descartes-Snell trouvée expérimentalement repose donc sur le principe de Fermat.
Pour la beauté de l'écriture, on appelle souvent i1 l'angle dans le milieu 1 et i1 l'angle dans le milieu 2.
La loi de la réfraction s'écrit alors:
n1 . sin i1 = n2 . sin i2
avec n1 = co/c1 = indice absolu du milieu 1. Et n2 = co/c2
On peut aussi l'écrire:
sin i1 / c1 = sin i2 / c2
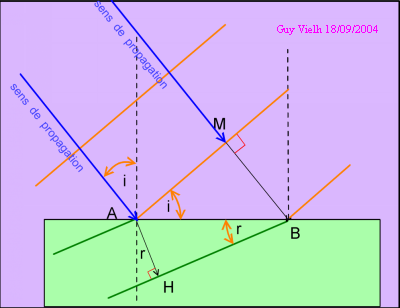
La lumière tourne parce que sa vitesse dans le milieu vert est plus petite que dans le milieu mauve.
Pour tourner avec un véhicule à chenillettes, on s'y prend exactement de la même manière: on ralentit l'intérieur du virage.
Naturellement, si la vitesse de la lumière dans le milieu vert était plus grande que dans le milieu mauve, la déviation serait dans l'autre sens, r serait plus grand que i.
Si on bien compris le principe de Fermat, la lumière met exactement la même durée pour parcourir AH et MB.
AH / c2 = MB / c1 (I)
Si on regarde les deux triangles AHB et ABM on peut écrire:
sin (i) = MB / AB
sin (r) = AH / AB
en utilisant la relation (I)
sin(i) = (AH . c1)/ ( c2 . AB ) = (c1/c2) . sin (r)
car AH / AB = sin(r)
le rapport des vitesses de la lumière dans le milieu 1 et dans le milieu 2, nous l'appelons "indice relatif du milieu 2 par rapport au milieu 1"
C'est bien long à écrire, on symbolise tout cela
