
Si a est une fonction linéaire du temps, le mouvement de M est circulaire uniforme.
a = w . t = 2 . p . f . t
w est la pulsation = 2 . p . f
xM = R.cos (2.p.f.t) et yM = R.sin (2.p.f.t)
Mieux encore: x est la partie réelle du nombre complexe:
R.ejwt (avec j² = -1)
et y en est la partie imaginaire
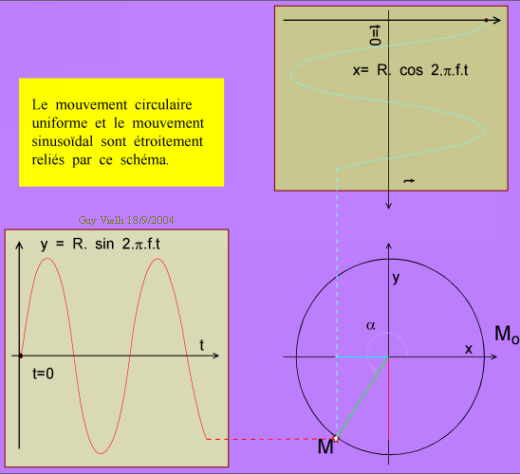
Deux mouvements : sinusoïdal rectiligne et circulaire uniforme entretiennent une relation intéressante.
Imaginons une roue (vélo par exemple) verticale sur sa fourche et qui tourne d'un mouvement uniforme. L'ombre de la valve portée sur le sol décrit un mouvement
dont l'équation montre une fonction trigonométrique. L'altitude de la valve a aussi une équation utilisant un sinus.
Étonnant ? Non : évident mais riche en possibilités ...
