Bref ... on voit que le secteur des vents contraires est plus grand que celui
des vents favorables ! Murphy a encore frappé .Sur fond vert, la relation v' = v - u : c'est le vecteur rouge.
Pour le cycliste, c'est la flèche rouge qui est le vent par rapport à son référentiel. Le vent actuellement est contraire !
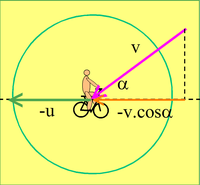
Que vaut alim ? v.cos alim = u
Il y a des cas où aucune solution n'existe si u > v on aura toujours le vent dans le pif!
Si on est à l'arrêt u = 0 le secteur rose et le secteur vert seront égaux.
Bref ... on voit que le secteur des vents contraires est plus grand que celui
des vents favorables ! Murphy a encore frappé .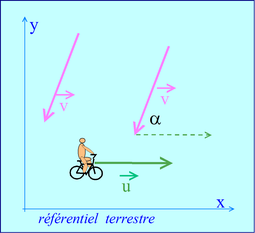
Projetons sur l'axe pointillé qui est la trajectoire du cycliste: Pour que le vent soit favorable, il faut que v.cos a - u soit positif :
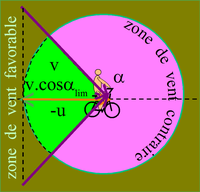
Nous voici dans un cas où, toute paranoïa mise à part, nous pouvons comprendre la version locale du principe de Murphy.
En effet, lorsqu'on fait du vélo, on trouve que, presque toujours, le vent nous est contraire.
v = vitesse du vent dans le référentiel terrestre (bleu).
u = vitesse du vélo dans le référentiel terrestre (bleu)
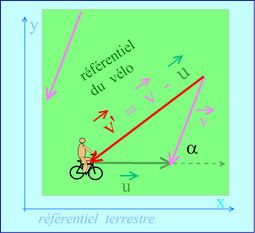
v' = vitesse du vent dans le référentiel du vélo (vert) .
Nous sommes exactement dans le cas exposé par la fiche précédente:
v' = v - u petit rappel, les lettres rouges sont des vecteurs !!!
Voyez l'élégance de la notation en vecteurs: une seule équation au lieu de trois en coordonnées cartésiennes avec x y et z .
