d) Pour le fondamental:
L' = v/2f1 = 343/(2 x 147) = 1,16 m (= le double)
e) D'après la loi donnée dans l'énoncé, la célérité du son augmente avec la température: Si on veut garder la même fréquence, il faut allonger le tube (relation (I))
en vertu de la relation II
L'/L = (T'/T)0,5 donc
L' = 0,583x[(273+35)/(273+20)]0,5 =
a) Un tube ouvert à ses deux bouts donne des modes propres avec des noeuds aux ouvertures. On démontre que, entre deux noeuds successifs, on trouve un ventre. Ceci est un "fuseau" par analogie avec les cordes vibrantes. La longueur d'un fuseau est l/2.Comme l = v/f, le mode fondamental qui ne présente qu'un seul fuseau de longueur L
f1 = v / 2L relation (I)
ce qui nous donne, pour les harmoniques:
fi = i .v / 2L : i étant le rang de l'harmonique, nombre entier évidemment.
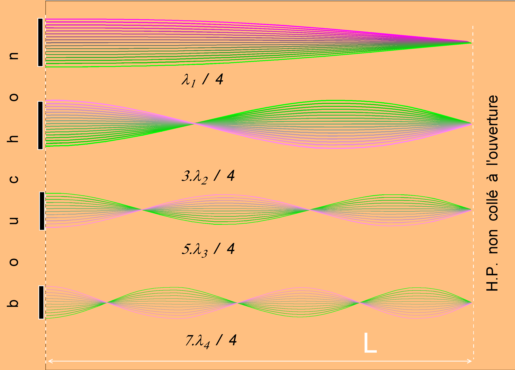
b) Pour le tuyau fermé à un bout: figure à droite
L = (2k-1)l/4 = (2k-1)v/(4fk) relation (II)
fk = (2k-1)v/(4L)
c) pour k = 1 , on a le fondamental 147 Hz on cherche
L = (2k-1)v/(4fk) = 343/(4 x 147 ) = 0,583 m harmonique 2 : f2 = 3x343/(4x0,583) = 441 Hz