A) L'activité d'un échantillon est le nombre de désintégrations par unité de temps:
A = - dN / dt
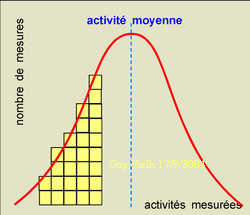
Une série de mesures sur un corps radioactif b- de taille modeste (compatible avec la protection contre les rayonnements dans un Lycée) montre que pour des tranches de temps dt identiques,
C) le raisonnement qui suit est valable pour la valeur moyenne. (ou pour une mesure effectuée sur un gros échantillon ou encore avec une durée assez grande).
Il est facile de montrer que l'activité est proportionnelle à la masse de l'échantillon: au nombre de noyaux N.
- dN/dt
= l . N
où l est la constante de proportionnalité ( = probabilité de désintégration) , elle dépend du nucléïde étudié. Puisque nous avons pris des précautions pour éliminer les fluctuations statistiques, rien ne nous empèche de dire que cette équation, lorsque dt devient infinitésimal est toujours correcte (pour la valeur moyenne) :
D) - dN/dt = l . N c'est une équation différentielle qu'on peut arranger en:
- dN/N = l dt
Sa solution est du type
Log( N/No) = -l . (t-to)
No est le nombre des noyaux radioactifs à la date to, N est le nombre des noyaux radioactifs présents à la date t. (prenons to = 0)
Elle peut s'écrire N/No = exp-l.t ou encore: N = No. exp -l.t
B) les activités qui devraient être les mêmes sont dispersées autour d'une valeur moyenne. Elles se distribuent selon une courbe en cloche (courbe de Gauss) caractéristique des phénomènes aléatoires.
Si on a un très gros échantillon de matière radioactive, l'activité mesurée plusieurs fois de suite donne toujours le même résultat :
