1) Au cours d'une éclipse totale de lune, la lune traverse le cône d'ombre de la terre.
En chronométrant la durée de ce phénomène, on a accès à la mesure du diamètre de la lune. On connaît le diamètre de la terre par la méthode d'Eratosthène.
Prenons l'exemple de l'éclipse totale de lune de 1997
2) On n'avait pas la chance que l'éclipse soit centrale. Entre 21h17min (sortie) et 19h8min (entrée) il s'est écoulé 7740s.
Sans se livrer à des calculs compliqués, avec un dessin à l'échelle fait à partir de photos, on peut établir le temps exact que la lune aurait mis à traverser cette ombre si elle l'avait fait selon le diamètre.
4). Comment calculer v ? C'est la distance parcourue divisée par la durée (Dt) . La distance parcourue est le diamètre de l'ombre de la terre (Fombre).
Elle est proche du diamètre de la terre(Fterre)
mais un peu plus petite parceque l'ombre derrière la terre forme
un cône. L'angle de ce cône est le diamètre apparent
du soleil 0,53° soit 9,33 .10-3 rad.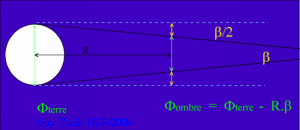
nous déduisons que Fombre = Fterre-R.b
5) v = Fombre / Dt = R.w
R(w.Dt + b) = Fterre avec les valeurs mesurées, on trouve:
R = 417 .103 km
Je ne veux pas avoir l'air de me
jeter des fleurs mais ... avec le peu d'investissement en matériel,
c'est un résultat excellent ! 
ben oui, des pensées cela me va !
3) Dt est cette durée = 8019 s
On connaît la période de la lune autour de la terre (T= 27,3 jours) et la relation qui lie la vitesse angulaire w et la vitesse curviligne v:
v =R . w =R.2.p/T
Mais nous pouvons obtenir v par une autre méthode, ce qui nous permettra de calculer R, rayon de révolution de la lune autour de la terre.
