 .W
.. . . . .Z
.W
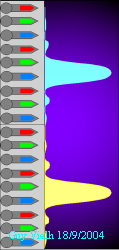
.. . . . .Z  La diffraction ne limite pas le pouvoir séparateur de l'oeil. Les
résultats sont cohérents: le pouvoir séparateur est
trois fois le diamètre apparent des cônes. Dans la figure
Z, on se trouve dans le cas limite: le cône rouge reçoit
très peu de lumière alors que les deux cônes bleu
et vert qui l'entourent sont bien éclairés. C'est avec peine
que l'on distingue que ce sont deux taches différentes. Par contre,
dans l'image W, les deux taches sont parfaitement résolues.
La diffraction ne limite pas le pouvoir séparateur de l'oeil. Les
résultats sont cohérents: le pouvoir séparateur est
trois fois le diamètre apparent des cônes. Dans la figure
Z, on se trouve dans le cas limite: le cône rouge reçoit
très peu de lumière alors que les deux cônes bleu
et vert qui l'entourent sont bien éclairés. C'est avec peine
que l'on distingue que ce sont deux taches différentes. Par contre,
dans l'image W, les deux taches sont parfaitement résolues.
 .W
.. . . . .Z
.W
.. . . . .Z  La diffraction ne limite pas le pouvoir séparateur de l'oeil. Les
résultats sont cohérents: le pouvoir séparateur est
trois fois le diamètre apparent des cônes. Dans la figure
Z, on se trouve dans le cas limite: le cône rouge reçoit
très peu de lumière alors que les deux cônes bleu
et vert qui l'entourent sont bien éclairés. C'est avec peine
que l'on distingue que ce sont deux taches différentes. Par contre,
dans l'image W, les deux taches sont parfaitement résolues.
La diffraction ne limite pas le pouvoir séparateur de l'oeil. Les
résultats sont cohérents: le pouvoir séparateur est
trois fois le diamètre apparent des cônes. Dans la figure
Z, on se trouve dans le cas limite: le cône rouge reçoit
très peu de lumière alors que les deux cônes bleu
et vert qui l'entourent sont bien éclairés. C'est avec peine
que l'on distingue que ce sont deux taches différentes. Par contre,
dans l'image W, les deux taches sont parfaitement résolues.

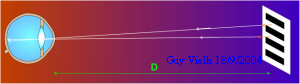
 Une
grille zébrée est affichée au mur
Une
grille zébrée est affichée au mur