 .
. 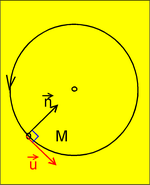

Schéma rouge .
la dérivée de v par rapport au temps est l'accélération a , c'est la tangente au cercle des vitesses. Nous avons a = v . w
a = v . w. = r.w . w = r . w²
or w = v / r donc : a = v²/ r
a est perpendiculaire à v : sa direction est le rayon de rotation, son sens est : vers le centre de rotation C. C'est cela que veut dire "centripète".
Comme on l'a vu l'accélération tangentielle est nulle, a = accélération centripète pure.
Pour un mouvement circulaire uniforme, l'accélération est centripète et a comme grandeur :
a = v²/ r
Pour un mouvement quelconque, on projette la vitesse sur la base de Frenet, on a deux accélérations mais l'accélération centripète a toujours la même expression. Le résultat est général.
 .
. 

Considérons un mouvement circulaire uniforme dans un référentiel galiléen naturellement.
Uniforme = la grandeur de v est constante donc v = v . u
avec u = vecteur tangent au cercle trajectoire du mobile et v = grandeur de la vitesse v.
En dérivant v nous obtenons le vecteur accélération : a = dv / dt = dv/dt.u + v. du/dt
or, si dv/dt = 0, ce n'est pas le cas de v.du/dt !!! ( rappel : symboles rouges = vecteurs )
du/dt = taux de variation du vecteur tangent à la trajectoire = n : schéma jaune.
Le vecteur a est perpendiculaire à v .
Le mobile M tourne à la vitesse angulaire w .
Nous avons v = r . w . (schéma mauve). Si nous portons les vecteurs vitesses sur un autre dessin: nous voyons le vecteur vitesse décrire un cercle de rayon v à la vitesse angulaire w .