En diaphragmant (en éliminant les rayons trop éloignés
de l'axe optique c'est à dire en respectant les conditions de Gauss)
la sphère est un bon dioptre pour réaliser des lentilles optiques.
Lorsque les rayons lumineux s'écartent des conditions de Gauss, cela se paye par l'apparition du défaut aberration de sphéricité parceque les rayons passant trop loin du centre de la lentille ne convergent pas au point image donné par les rayons centraux.
En diaphragmant (en éliminant les rayons trop éloignés
de l'axe optique c'est à dire en respectant les conditions de Gauss)
la sphère est un bon dioptre pour réaliser des lentilles optiques.
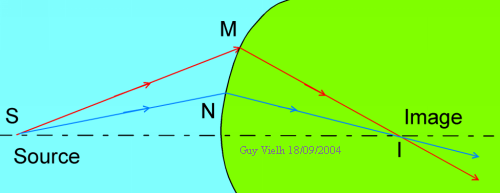
Les chemins SMI et SNI doivent prendre le même temps. Dans la zone bleue la lumière circule à la vitesse c1 et dans la zone verte la lumière se propage à la vitesse c2.
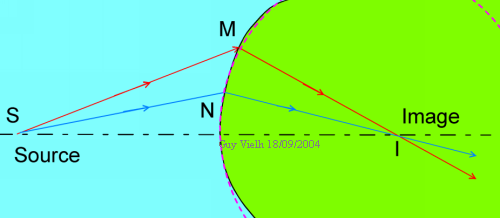
La lumière emprunte le chemin qui lui demande le moindre "temps de vol". C'est le principe de Fermat.
Dans un dioptre, si on veut qu'il y ait focalisation de la lumière, tous les rayons issus d'un point lumineux objet doivent se couper en un point unique: l'image.
La surface obtenue n'est pas une sphère mais une chose très compliquée du 4° degré.
Impossible à tailler avec des machines dans des conditions économiques acceptables pour la quasi totalité des applications.
Si on accepte de limiter le foncionnement du dioptre aux conditions de Gauss, il se trouve que la surace sphérique est convenable.
C'est une approximation qui est presque parfaite en diaphragmant pour ne laisser passer que les rayons centraux.