Or la lumière frappe la totalité de la goutte: il faut comprendre ce que fait toute la lumière qui entre dans la goutte ...
Plaçons nous au point de sortie du rayon de classe 3 : D = p - D
b + D + i' = p
or sin i' = n . sin r (Descartes Snell) donc i' = q
D = p - p - i' - b soit :
D = p + 2.q - 4{ Arcsin[sin(q)/n]} (angles exprimés en rad)
D = 180 + 2.q - 4{ Arcsin[sin(q)/n]} avec les angles exprimés en degrés.
ça c'est de la formule !!!
Or la lumière frappe la totalité de la goutte: il faut comprendre ce que fait toute la lumière qui entre dans la goutte ...
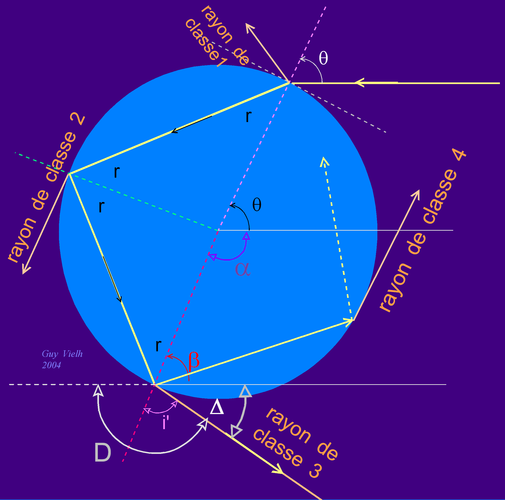
On cherche à exprimer l'angle D dont la lumière de classe 3 est déviée de sa direction incidente.
En se plaçant au centre de la goutte,
q + a + 2.p -4.r = 2.p (donc a= 4.r - q)
Descartes-Snell nous donne la relation :
sin q = n . sin r
avec n = indice relatif de l'eau par rapport à l'air . La valeur est proche de 1,33 mais dépend de la longueur d'onde de la lumière: c'est
l'origine du phénomène de dispersion de la lumière.
Il existe une relation entre a et b qui sont des angles alternes internes : a + b = p
b = p + q - 4. Arcsin q