wo = 2.p.f (par définition)
nous trouvons que la fréquence avec laquelle oscille ce pendule de torsion sans frottement est:
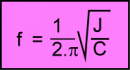
phase qui dépend de l'instant que nous choisissons comme origine des temps .
a' = w . A . cos ( w.t + f )
a" = - w² . A . sin ( w.t + f ) = - w² . a
L'équation différentielle devient :
- J . w² . a + C . a = 0
soit : w² = J / C
Cette pulsation sans amortissement et dite "pulsation propre" on la note wo .
Le mouvement est périodique avec
wo = 2.p.f (par définition)
nous trouvons que la fréquence avec laquelle oscille ce pendule de torsion sans frottement est:
.....
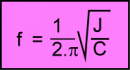
. Sur des horloges à balancier horizontal,
le mécanisme est apparent. On obtient facilement des périodes
de 20s. L'amortissement étant très faible, la consommation d'énergie
nécessaire à l'entretien du mouvement est très petite.
On ne remonte le ressort que tous les mois!
Lorsque le mouvement est entretenu, la fréquence est exactement celle que la résolution de l'équation différentielle donne dans cette fiche. On a coutume de lui mettre l'indice "o". On a donc wo² = J/C et ainsi de suite. Pourquoi cette réserve? Pour les mouvements non entretenus, le frottement complique un peu les choses. (comme pour le pendule à ressort, le circuit RLC libre ...)
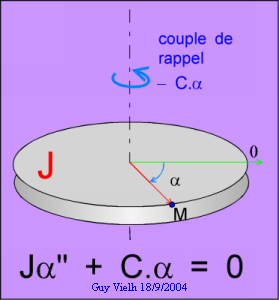
C'est le pendule de torsion. Un fil de torsion ou un ressort spiral assure un couple de rappel proportionnel à l'amplitude angulaire a.
La relation de la dynamique des corps en rotation indique que :
le moment du couple = J a" soit:
J . a" + C . a = 0
Ce type d'équation différentielle admet, comme solution une fonction trigonométrique de type "sin" ou "cos" car d²[sin(x)]/ dx² = - sin(x).
Allons-y-gaiement! a = A . sin( w.t + f )
A est l'amplitude maximale, nous supposons que l'amortissement est insignifiant. w est une constante à déterminer (pulsation) et f est la
