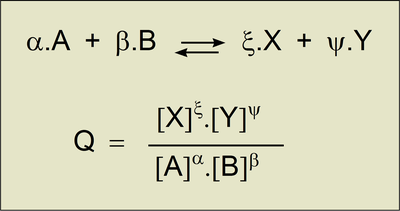K = xf²/(1-xf)²= 4 qui admet comme solution
xf = 0,666 mol.
Nous forçons l'équilibre en partant d'une grande quantité d'acide par exemple: 10 mol.
K = xf²/[(10-xf)(1-xf)]
En développant et ordonnant:
(K+1)xf² + 11.K.xf -10.K = 0
équation du second degré dont la racine positive (qui , seule, a une signification dans notre problème) est
xf = 0,83 mol .
On a donc déplacé l'équilibre sur l'alcool de 0,666 à 0,83 mol. Ce n'est pas négligeable mais on voit là la limite du procédé de forçage par abondance d'un des réactifs.
Tableau d'avancement de la réaction dans les conditions
stoechiométriques :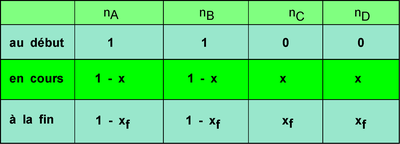
La résolution de l'équation donne xf = 0,667 mol.L-1
Tableau d'avancement pour la réaction forcée
sur le réactif A: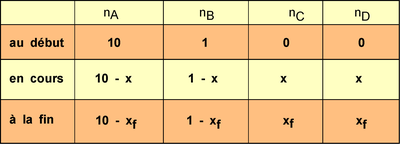 
La résolution donne xf = 0,83 mol.L-1
( on a considéré que comme le volume ne varie pas et vaut 1L, les quantités de matière "n" et les concentrations ont les même valeurs)
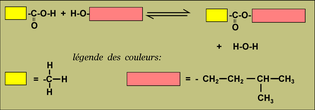
La constante d'équilibre est K = 4
Si on a introduit dans le réacteur 1 mol d'acide et 1 mol d'alcool dans un litre, on obtient combien d'ester et d'eau ?
Le tableau d'avancement permet de trouver les concentrations en fonction de xf , l'avancement final de la réaction. Les nombres stoechiométrique sont égaux à 1.
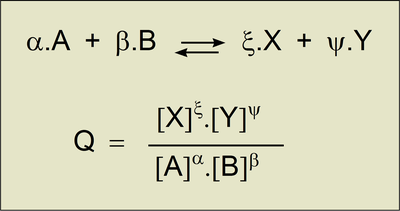
avec : a = b = x = y = 1
