
Lorsque (j1 - j2) = 0 , l'amplitude est maximale. C'est le cas, au centre de l'écran sur l'axe de symétrie.
On remarque que ce résultat est évident mais ça fait toujours plaisir de trouver laborieusement ce que notre esprit agile et paresseux avait entrevu dans un éclair.
Ce qui commande les valeurs de j c'est le temps de trajet du signal: c'est: distance parcourue / vitesse de l'onde.

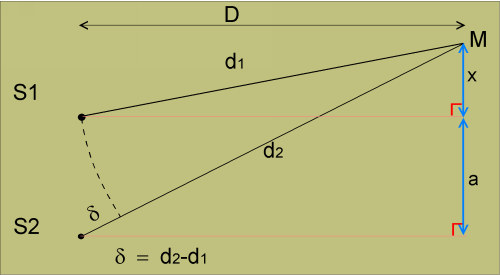
Pythagore dit que: (d1)² = D² + x² et aussi que (d2)² = D² + (a+x)²
par conséquent, (d2)² - (d1)² = a² + 2ax c'est aussi = (d1+d2)(d2-d1)
quelques approximations pour nous sortir d'une mauvaise situation mathématique: d1+d2 = 2D (ou presque!) parce que D>> (a+x). Pareillement, si x est beaucoup plus grand que a (dans le cas de l'optique c'est très vrai, sur la cuve à ondes ça se discute ...) a² << 2ax.
Il reste 2ax = 2D.d soit x = D.d /a . Lorsque d = k.l l'amplitude est maximale: il y a de la lumière, les vagues sont fortes. x = k.l.D/a. Lorsqu'on fait augmenter x, la région éclairée suivante est obtenue pour d' = (k+1)l . . Cela nous donne x' = (k+1).l.D/a.
Si on fait x'-x on trouve que l'interfrange est de i = l. D / a.
L'interfrange est la distance qui sépare deux régions consécutives où il y a du signal.
Les ondes ont une évolution temporelle sinusoïdale, on peut écrire facilement leurs équations: dans le plan qui contient les deux sources, pas trop loin de l'axe et à bonne distance, on peut considérer que les deux amplitudes maxi sont les mêmes: A.
L'onde de la source S1:
A1 = A.sin( w.t + j1)
l'onde de S2:
A2 = A.sin( w.t + j2)
Au point que nous étudions, l'amplitude résultante est A1 + A2 soit:
A.{sin( w.t + j1) + sin( w.t + j2)} =
2A{sin[wt+(j1 + j2)/2] . cos[(j1 - j2)/2]}