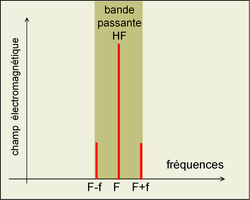
une bande de fréquence de largeur 880 Hz (2f) centrée sur la fréquence de la porteuse.

Aucun autre émetteur ne doit empiéter dans cette bande sous peine d'être pris (à tort) pour le signal utile.

La situation devient sérieuse si nous considérons (ce qui était notre premier objectif)

que le signal est de la musique.

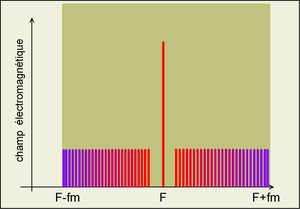
Alors il va contenir de nombreuses fréquences dont la plus élevée va déterminer la bande passante du signal (f_m) et la bande passante HF = 2f_m.

 

La tension modulée est un machin complexe. On se demande ce qu'il contient exactement. Que voit-on dans son spectre?

u_s(t) = A.[m.cos(2pf_s.t)+1]cos(2pF.t)

u_s(t) = A.m.cos(2pf_s.t).cos(2pF.t)+A.cos(2pF.t)

Développons le terme vert: A.m.cos(2pF.t).cos(2pf_s.t) c'est un produit de deux cos : nous connaissons une relation en math :cos(a).cos(b) = 0,5.cos(a+b)+ 0,5.cos(a-b)

cela donne 0,5.A.m.cos[2p(F-f)t] + 0,5.A.m.cos[2p(F+f)]

u_s(t) = 0,5.A.m.cos[2p(F-f)t] + A.cos(2pF.t) + 0,5.A.m.cos[2p(F+f)]

Voilà: le signal modulé contient trois fonctions périodiques sinusoïdales, le spectre de ce signal modulé est donné à droite: Il contient trois raies d'intensité 0,5A.m ; A ; 0,5A.m

Dans notre exemple, f = 440 Hz cela occupe

Bande passante du signal et du signal modulé