image
1 ....................................................
image 2.
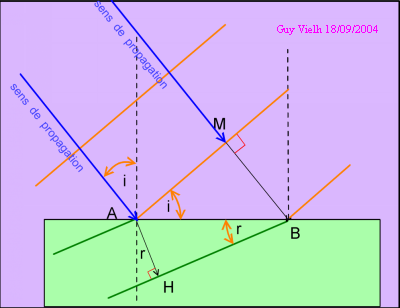 .
image 3......
.
image 3......
La perturbation qui était en A est maintenant
en H. La durée dt écoulée
étant la même, nous avons : MB = dt
. C1 et AH = dt . C2.
Pourquoi le chemin suivi est-il la perpendiculaire
aux fronts d'onde? Parce que c'est le chemin qui prend le moins de temps:
dans chaque milieu homogène c'est le plus court. (merci qui? merci
monsieur Fermat).
Dans le triangle ABH : AB
= AH / sin(r) = dt
. c2 /sin(r)
Dans le triangle ABM : AB
= MB / sin(i) = dt
. c1 / sin(i)
or AB est le même! Donc c2/sin(r) = c1/sin(i)
ou encore sin(i) = c1/c2 . sin(r) mais
... c'est la relation D2 !!!
En prime, nous savons maintenant que l'indice n2/1
= c1/c2. Les démonstrations, cela prend quelquefois
la tête, mais on en obtient des résultats intéressants.
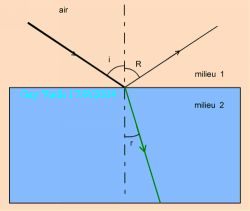
Voyons à présent la réfraction sur un dioptre .
La lumière subit la réfraction en passant d'un milieu dans
lequel sa célérité est c1 à un autre milieu dans
lequel sa célérité est c2. La loi:
sin (i) = n2/1 . sin (r) (D2)
Ce que l'on voit au laboratoire avec le matériel géoptic
et donné dans l'image 2. Nous savons que, dans le plexiglass, la célérité
de la lumière est plus petite que dans l'air.
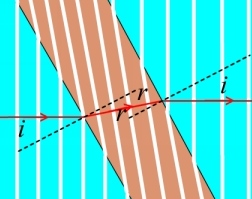
Sur la cuve à ondes, on observe la réfraction sur un dioptre:
un haut fond ralentit la vitesse de propagation des ondes: la direction
de propagation est déviée (images 1 ).
Le principe de Fermat entraîne-t-il la deuxième loi de Descartes
(D2)
L'image 3 correspond à deux photos superposées: la première
montre l'onde incidente et deux points A et M de cette onde plane.
La deuxième, l'instant où l'onde atteint B. La perturbation
de M est en B.


 .
image 3......
.
image 3...... 



