z est l'altitude et a une relation avec x :

z = zo + x la proportionnalité entre l'allongement lo et le poids ( m.g = k.lo) permet d'écrire également:

lo = m.g/k

On fait la somme des trois énergies:

E = Epr + Epg + Ec

C'est un travail de nettoyage et d'ordonnancement qui aboutit à :E = 0,5.k.x²max.(sin²+cos²) + 0,5.k.l²o + m.g.zo

On voit que E = constante.

Le terme m.g.zo dépend du choix de l'altitude de référence, on peut choisit zo = 0. Quant à 0,5.k.l²o c'est l'énergie potentielle emmagasinée lors de la suspension de la masse m au ressort.

Avec l'expression de x et x' en fonction du temps :

Ec = 0,5 . m . w_²o.x_²max.sin²(w_ot) ; Epr = 0,5 . k . (x + m.g/k)² ;

Epg = m.g.(zo+ x_max. cos(w_ot)) .

Dans les deux pages "pendule vertical 1 & 2" on a résolu l'équation différentielle qui décrit le mouvement de ce pendule dans la cas "sans frottement".

Elle nous fournit les équations suivantes:

x = x_max. cos(w_ot)

si on choisit de lâcher le pendule dans sa position extrême en haut au déclenchement du chronomètre.

Alors la vitesse x' = -w_o.x_max.sin(w_ot) ................. avec w_o² = k/m

et l'accélération x"= -w_o².x_max.cos(w_ot) .

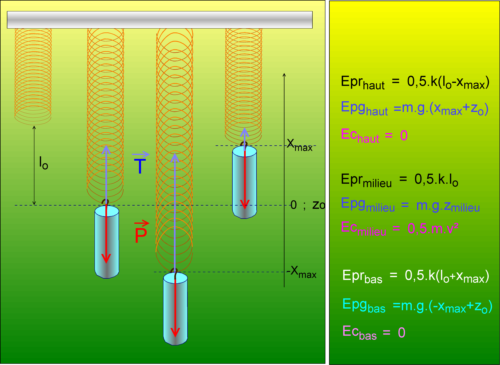
Où se trouve l'énergie ? Dans trois "réservoirs" :

Ecinétique = 0,5 . m .x'²

Epot-ressort = 0,5 . k . (x + lo)²

Epot-gravité = m . g . z

Pendule vertical: échanges d'énergie (idéal)