jusqu'à la valeur finale i = n. Cette opération lorsque les dti sont infinitésimaux est une intégration.
WB - WA = 0.5 . m ( vB² - vA² )
Newton (loi n°2 ) dit :
m.ai = Fi mais ai = dvi / dti (c'est l'accélération)
or dWi = Fi . dsi (c'est la définition du travail) et vi = dsi / dti (c'est la définition de l'accélération)
remplaçons dWi = m . ai . vi . dti
remplaçons encore ai par dvi/dti:
dWi = m . dvi . vi dti/dti
dWi = m . dvi . vi
Pour trouver le travail total de la force entre les points A et B, y'a qu'à ajouter tous les dWi à partir de i = 1
jusqu'à la valeur finale i = n. Cette opération lorsque les dti sont infinitésimaux est une intégration.
WB - WA = 0.5 . m ( vB² - vA² )
Pour un solide en translation dans un référentiel galiléen, la somme des travaux forces extérieures est égale à la variation de l'énergie cinétique sur un parcours AB.
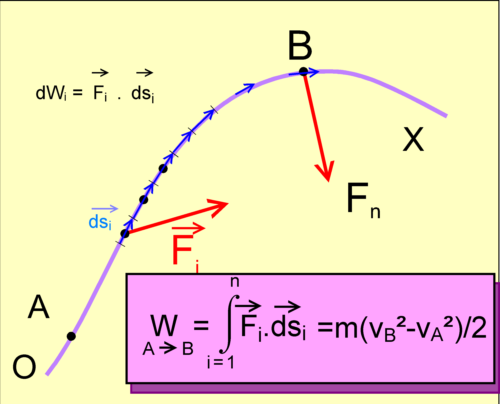
Le théorème n'est pas un principe, un théorème cela se démontre.
Cramponnez vous.
Soit un solide de masse m, dans un référentiel galiléen. Ce solide n'a pas de mouvement propre de rotation (sinon il faut aussi s'occuper
du moment cinétique et ceci est une autre histoire).
Autrement dit, ce solide est en mouvement de translation. Sur lui s'exercent des forces (extérieures) dont la somme est F . (caractères rouges = vecteur). F n'est pas tenue d'être constante sur le parcours AB que nous
étudions. Mais nous allons découper ce parcours en autant de petits intervalles qu'il le faut pour que, sur chaque intervalle ds, parouru dans la durée dt, on puisse considérer que F reste constante. On va numéroter ces intervalles (en mettant un indice "i")
Regardons l'intervalle "i", la force est Fi , le vecteur déplacement dsi la durée dti.