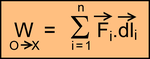
si les intervalles sont infinitésimaux, il faut écrire:
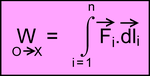
Si le force varie n'importe comment ainsi que la trajectoire ... bien du plaisir !
Mais en physique la trajectoire et la force ne varient en général pas n'importe comment. Elles sont décrites par des équations pas très compliquées.
La sommation devient possible.
De toutes façons avec un ordinateur on peut toujours faire ce sale boulot dans tous les cas.
Enfin ... BREF, l'opération porte le nom d'intégration.
On l'écrit:
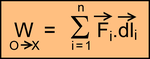
si les intervalles sont infinitésimaux, il faut écrire:
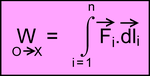
Autour du point A, on détermine l'intervalle
dl qui est un vecteur de sorte que FA ne change pas. Le travail
élémentaire dWA est rigoureusement donné
par la relation sur fond vert. L'intervalle est aussi petit que nécessaire
(on dit qu'il peut devenir INFINITÉSIMAL).
Au final, on somme tous les travaux élémentaires : dWA + dWA' + dWA" + ... + dWB + ... + dWC + ....
Comme on le voit dans la fiche précédente, pour un déplacement selon un vecteur, le travail est donné par le produit scalaire de la force par le vecteur déglacement.
W = F . l . cos (a)
Mais lorsque la force évolue ou/et que le déplacement n'est pas un vecteur rectiligne ... Cela se complique un petit peu.
On s'en tire en découpant en autant d'intervalles aussi petits qu'il le faut pour que, sur chaque intervalle ni le vecteur force, ni le vecteur déplacement ne changent:
alors, pour chaque intervalle, on peut écrire rigoureusement :
Pour avoir le travail tout le long du trajet, il "n'y a qu'à faire la somme" de tous les travaux élémentaires sur chaque intervalle.
