 .
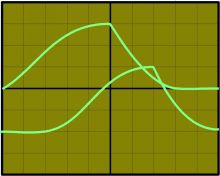
écran idéalisé de l'oscilloscope.
.
écran idéalisé de l'oscilloscope.
Dt = 2 div . BdT
La précision de cette méthode n'est pas formidable: L'incertitude dl sur l , lu sur l'écran est de ± 0,2 div :
tl = 0,2/2 = tDt = ± 10 %
td = 0,1/20 = ± 0,5 %
tc = 10,5 %
Avec un résultat de 3.108 m.s-1 il faut écrire:
c = 3 ± 0,3 .108 m.s-1
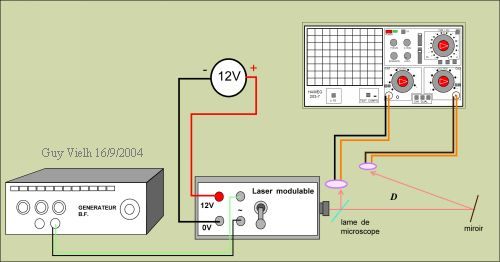
pour une mesure D = 20 m.
C'est encore pire que cela: lorsqu'on trouve 2. 108 m.s-1 on est content!
Hélas, on travaille dans des conditions limites, en particulier parce que le laser est poussé dans ses retranchements: On lui demande de s'allumer et de s'éteindre à 1 MHz et il n'a pas le temps d'atteindre sa luminosité. Le signal de retour est très faible, la moindre vibration (il suffit de bouger ou de parler dans la pièce) fait tanguer le signal au point où il est quasiment impossible de lire l'écran de l'oscillo.
Il faudrait augmenter le trajet de la lumière: si on lui faisait parcourir 200m soit 10 fois plus, on reviendrait dans la zone de performance des appareils à notre disposition.

 .
écran idéalisé de l'oscilloscope.
.
écran idéalisé de l'oscilloscope.
Dt = 2 div . BdT
Le signal lumineux a parcouru D en une durée Dt à la vitesse "c" de la lumière dans l'air .
c = D / Dt