Cette question est le "paradoxe d'OLBERS"
La nuit le ciel est noir, sauf les étoiles et les planètes.
Pourquoi, si l'Univers est infini y aurait-il des directions sans la moindre étoile ?
Sous cette forme la question semble moins facile .
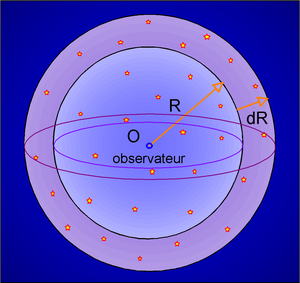
B) V = 4 p R² . dR ; le nombre d'étoiles = 4 p R² . dR . r
La quantité de lumière reçue par l'observateur en provenance de la couche mauve est proportionnelle à 1/R² donc: à 4 p R² . dR . r / R² . Donc, la quantité de lumière ne dépend pas de R. Pour avoir la quantité totale de lumière provenant de l'univers entier, on somme toutes les contributions des couches successives (on intègre sur dR jusqu'à l'infini) c'est une valeur infinie! En vérité, comme les étoiles ont un certain diamètre apparent et qu'elles sont opaques, lors de la sommation, quand toute la voûte céleste est recouverte de disques stellaires, la lumière venant d'étoiles plus lointaine ne peut nous parvenir. La luminosité n'est pas infinie: c'est la luminosité de la surface du soleil. Partout, de jour comme de nuit !!!
A) Hypothèses: l'Univers est infini (H1) , éternel (H2) et régulièrement peuplé d'étoiles (H3). Nous pouvons montrer que cet univers présente(rait) un ciel brillant comme la surface du soleil. Partout, de jour comme de nuit.
Découpons, par la pensée, l'univers en couches concentriques comme un oignon. Dans la peau d'oignon mauve, il y a des étoiles. Combien ? Puisque l'univers est uniformément peuplé, le nombre d'étoiles de la couche mauve est le volume x densité. Notons la densité "r".
Le volume de la couche mauve » surface de la sphère bleue x dR (si dR est petit devant R) .