1.d: vous ne pouvez pas balancer la formule assortie de "on sait que" ; ça n'est pas un raisonnement. Vous répétez quelque chose qui n'est pas forcément pertinent dans la situation du problème.

Il faut l'établir cette "formule".

1.f : Par définition les harmoniques ont leurs fréquences régies par la loi:

f_n = n . f₁

alors, pour n=5 : f₅ = 5 x 80 = 400 Hz

1.g : par définition deux notes i et j présentent un intevalle d'une octave

si f_j/f_i = 2

Dans la question c'est le cas 160/80 = 2. La réponse est positive.

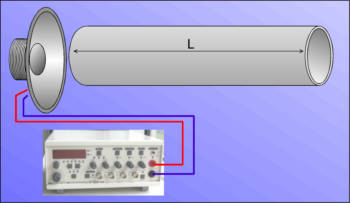
Démonstration de la "formule-qui-permet-de-résoudre-tout".

Pourquoi y a-il onde stationnaire ? Parce que l'onde qui se réfléchit à l'extrémité droite qui s'inverse, revient, se réfléchit sur l'extrêmité gauche, s'inverse encore (elle est donc identique à celle produite par le HP) est parfaitement en phase avec celle produite par le HP lorsqu'il y a résonance. Alors, ces deux ondes se renforcent. (sinon elles se contrarient).

Cela ne se peut que si le temps de trajet sur la corde est un multiple entier de la période.

dt = 2.L / v = n.T Il est temps de se souvenir que "par définition" T = 1/f et aussi que l = v.T

alors, en combinant ces relations, il vient : 2.L/ v = n.T = n / f_n = relation (E)

Cela peut s'écrire v = 2.L.f_n / n ce qui donne la réponse à la question 1.d en remarquant que le fondamental c'est lorsque n=1. Mais cela marche aussi pour les harmoniques.

On trouve v = 320 m.s-1 . Dans (E), on y voit aussi que L = n . l / 2 .

Pour voir les fuseaux: cliquez ici.............................

L'énoncé donne la situation: la même qu'une corde vibrante tenue à ses extrêmités.

Le schéma:

 

1b : fréquences propres ou bien fréquences des modes propres.

1.c: la fréquence la plus basse est celle du mode fondamental nous la noterons f₁. Comme d'habitude!

CORRIGE SPE1 de novembre 2005