mode RUN :
[touche racine carrée][OPTN][F1][F1][2][->][F1] [4][EXE]
done . En revenant en mode STAT, constatez que la liste 4 est garnie des racine carrée des valeurs de la liste 2
Y'apluqu'à faire tracer en GRAPH2
X = list 4
Y = list 3
on obtient l'écran 2
1 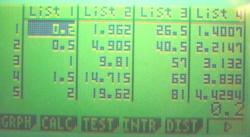 .
.2 .
.
.2 . . .3. .
. .3. .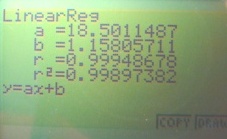 .
.4 .
.
.4 . 
f en fonction de racine carrée de F montre des points alignés. De sorte que la loi est f = 18,5 . (F)0,5 + 1,15 mais la demi-droite idéale devrait passer par l'origine, b doit être nul.
La régression en PWR sur la page précédente donnait f = 19,5 . (F)0,5. Si on traçait le graphe à la main, on imposerait b = 0. Voici pourquoi je fais confiance à 19,5.(F)0,5.
Comme v = 2Lf , le graphe de v en fonction de X = (F)0,5 est également une droite. Son équation est v = 21,8. (F)0,5.
Mais l'énoncé nous demande de faire une méthode particulière: c'est celle exposée dans la première partie. Il sera prudent, le jour de l'examen de suivre les consignes.Car le barrème de notation est extrêmement pointilleux et vous devez ramasser le maximum de points.
Par contre, si c'est un concours d'entrée dans une
classe prépa, ne vous privez pas de montrer que vous savez maîtriser les possibilités de la calculette.
Pour suivre les demandes: on vous "conseille" de tracer un graphique après avoir fait un changement de variable. Comment obtenir une droite, en remplaçant Fi (en abscisse) par Xi.
A ce point du problème, vous savez que c'est (Fi)0,5 qu'il faut utiliser.
Pour le tracer avec vos petits doigts, c'est possible mais avec la calculette aussi:
En suivant la même procédure, fourrez dans la liste 4 la racine carrée de la liste 2 ( puisque c'est là que se trouvent les valeurs de la tension de la corde)