En plaçant en abscisse non pas m mais (m)-0.5 on doit obtenir une droite.
en mode RUN calculons (m)-0.5 et versons le résultat en liste 3 puis faisons tracer list 2 en fonction de list 3. c'est l'écran 6.
Cette demi droite a comme équation
f = 0,36 .(m)-0.5 en négligeant b = -0,12
comme v = 2Lf, v est aussi proportionnelle à (m)-0.5 et son graphe est une demi-droite.
1 2
2 3
3 4
4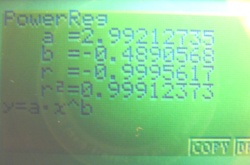 5
5 6
6
Exploitation de l'expérience 2. Influence de la masse linéïque sur la fréquence.
C'est le même déroulement que pour la question b .
Faisons le travail directement avec la calculette: on entre dans la liste 1 la masse linéïque m et dans la liste 2 la fréquence qui donne un seul fuseau.
On aurait certainement eu plus d'efficacité à traiter non pas les fréquences mais les vitesses de propagation v. Le problème est tourné ainsi pour que les gens qui se sont plantés dans la question a puissent se relancer.
écran 1 : l'entrée des valeurs.
écran 3 : les points f en fonction de m ne sont pas alignés.
écran 4: la régression PWR dénonce la relation avec b = -0,5 . par conséquent :
f = 3 . (m)-0.5 ce qui s'exprime: la fréquence du fondamental est inversement proportionnelle à la racine carrée de la masse lineïque de la corde.