Développons le terme vert: A.m.cos(2pF.t).cos(2pf_s.t) c'est un produit de deux cos : nous connaissons une relation en math =

cos(a).cos(b) = 0,5.cos(a+b)+ 0,5.cos(a-b)

cela donne 0,5.A.m.cos[2p(F-f)t] + 0,5.A.m.cos[2p(F+f)]

Moralité: u_s(t) = 0,5.A.m.cos[2p(F-f)t] + A.cos(2pF.t) + 0,5.A.m.cos[2p(F+f)]

Trois tensions sinusoïdales composent le signal modulé émis par l'antenne.

Le spectre contient trois raies, la raie centrale plus intense que les deux raies latérales.

Avec les valeurs de l'énoncé:

u_s(t) = 0,75.cos[2p(4900)t] + 3.cos(2p5000.t) + 0,75.cos[2p(5100)]

vers problème 15

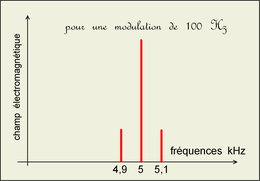
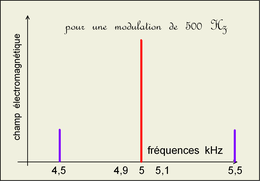
Modulation à 100 Hz: l'exercice mais dans le cas d'une modulation à 500 Hz les raies latérales s'écartent (de la différence F-f)

Pour une modulation musicale qui ne contiendrait que les fréquences entre 25 et 500 Hz, on a des "bandes latérales". Une station occupe totalement une bande de 2f de largeur centrée sur la fréquence de la porteuse. (voir exercice 12)

On montre que (exercice 12)

u_s(t) = A.[m.cos(2pf_s.t)+1]cos(2pF.t) ; (I)

u_s(t) = k.Pm.U_o {Sm_/U_o[cos(2pf_s.t)]+1} . cos(2pF.t)

en posant A = k .Pm.U_{o et m =} Sm_/U_o

L'énoncé indique que:

A = 3 V; m = 0,5 ; 2F = 10000 Hz ; 2f = 200 Hz

a) F = 5000 Hz

b) f = 100 Hz

c) m = 0,5

d) à partir de (I), développons

u_s(t) = A.m.cos(2pf_s.t).cos(2pF.t)+A.cos(2pF.t)

Le terme rouge est la première des tensions demandées.

N°13 Spectre de fréquences