Le vecteur vitesse change linéairement selon l'axe oz uniquement:

d(OM)/dt = i.v_ox + j.v_oy + k.(a.t + v_oz)

v_ox , v_oy et v_oz sont les trois composantes de la vitesse initiale ( instant t = 0). Si la vitesse initiale est horizontale, seule v_ox n'est pas nulle.

 

OM = (v_ox . t + x_o). i + (v_oy . t + y_o). j + ( 0,5. g t² + v_oz . t + z_o ). k

Le point Mo de coordonnées x_o , y_o , z_o est l'emplacement du mobile lorsqu'on lâche la bille et déclenche le comptage du temps t. On y place l'origine de notre repère .

OM = (v_ox . t ). i + 0. j + ( 0,5. g t² ). k

On démontre ainsi le mouvement uniforme selon l'axe ox horizontal et le mouvement uniformément accéléré vertical. Le coefficient

0,5.g = 4,9 N.kg^-1

On lance un mobile qui est soumis à une force dérivant d'un champ uniforme. La force a toujours les mêmes caractéristiques (direction, sens, grandeur) : c'est le poids

La relation fondamentale de la dynamique dit que : si le référentiel est galiléen,

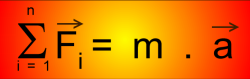Rien ne nous empêche de choisir un repère dans le référentiel galiléen avec un axe parallèle à la direction du vecteur accélération. Et l'autre dans la direction de la composante horizontale

de la vitesse. Exemple :

d²(OM)/dt² =i.d²x/dt² + j.d²y/dt² + k.d²z/dt² = k.a

dans le cas de la pesanteur.

d²x/dt² = 0 et aussi d²y/dt² = 0

par contre d²z/dt² = a = g = 9,8 N.kg^-1 ou m.s^-2

CHUTE LIBRE avec vitesse initiale horizontale.