 ......
......
La particule est déviée perpendiculairement à sa vitesse. Il n'y a aucune accélération selon la trajectoire. La vitesse tangentielle est constante. Seule l'accélération normale à la trajectoire a une valeur:
a = F/m = qvB/m. Dans le repère de FRENET : a = v²/r (r est le rayon de courbure local de la trajectoire)
Mais comme v reste constant en grandeur, r garde sa valeur vo: le mouvement est un cercle.
Quelle surprise...La particule décrit un cercle dont le rayon est:
r = mvo /(qB)
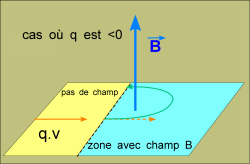
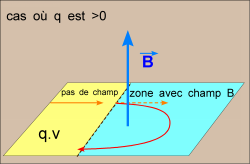
Le sens dans lequel la trajectoire s'enroule dépend du signe de q .
Pour un électron, il s'enroule dans le sens trigo lorsqu'on voit venir le champ B vers nous..
Une particule chargée entre dans un champ magnétique B uniforme avec la vitesse vo. . Pour simplifier la particule est injectée perpendiculairement au champ.
La force F = q.v ^ B (en rouge = vecteurs) Le sens et la direction de cette force sont donnés par la règle des trois doigts
La force F est normale à B et à v.
Choisissons un référentiel galiléen. Puisque la vitesse initiale est perpendiculaire à B, F est perpendiculaire à B et à la vitesse vo.
La relation fondamentale de la dynamique dit que l'accélération = force divisée par la masse
de la particule: a = F/m . Il n'y a aucune accélération selon la direction du champ magnétique. Par conséquent, l'instant suivant, aucune vitesse et aucun déplacement selon la direction de B.
De proche en proche, on voit que le mouvement de la particule reste dans le plan perpendiculaire à B: la trajectoire est PLANE.