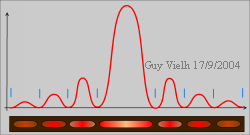
Voilà le monstre sympathique. En dessous: ce que
l'on voit sur l'écran.On voudrait bien voir quelle tête elle a, cette équation. Il faut exprimer F en fonction des grandeurs mesurables sur la table d'expérience. (Schéma 3). Il n'y a plus qu'à tracer ce petit monstre avec la calculette.
I = 4.Io.[sin²(p.x.a/lD)]/[2.p.a.x/(D.l)]²
Lorsque F = p , I est nulle. Ceci se produit lorsque x = L/2 et -L/2 . Cela conduit à L = 2.l.D/a.
Voilà le monstre sympathique. En dessous: ce que
l'on voit sur l'écran.
En bleu, les traits avec lesquels on relève les figures de diffraction dans l'expérience de la mesure du diamètre d'un cheveu.
schéma3
a = largeur de la fente. D = distance entre la fente et l'écran. x = distance au centre de l'écran du point que nous étudions, nous regardons l'expérience par dessus, la fente est verticale et x selon l'horizontale.
Dans le cas de la diffraction par une fente, nous ignorons la valeur de n et la valeur de p (qui est le pas du réseau).
Ne nous laissons pas démonter: il y a n sources et ce nombre, nous allons le faire tendre vers l'infini. "n" disparaît: notre résultat est valable aussi bien pour le fil que pour la fente.
............................................................................ ...
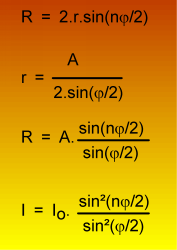
nj = F . La dernière équation sur fond jaune se transforme comme on le voit dans le cadre bleu . Nous obtenons une équation dans laquelle n a disparu! Formidable!
