avec le signe opposé, que l'on peut espérer obtenir 0?: sin ou cos !
x = Xmax . sin (wot) alors
x' = wo.Xmax cos (wot) et enfin
x" = - wo²
. Xmax sin (wot) 
m.x" + k.x = 0
ou encore: x" + (k/m).x = 0
Cette équation différentielle, on sait la résoudre.
Quelle est la fonction dont la dérivée seconde lui ressemble tellement
avec le signe opposé, que l'on peut espérer obtenir 0?: sin ou cos !
x = Xmax . sin (wot) alors
x' = wo.Xmax cos (wot) et enfin
x" = - wo²
. Xmax sin (wot)
x"= -wo² . x on voit donc que
wo² = k/m
Bon d'accord, on n'a pas pris en compte les frottements. Alors disons que si tout était parfait (pas de frottement ou un mécanisme entretenant l'énergie) le système oscillerait avec la pulsation wo .
Ce que l'on mesure avec le chronomètre est la "pseudo-période" .
L'emmerdeur: "et si on tenait compte de l'amortissement, peut-on rendre l'usure progressive de l'amplitude (Xmax) et la petite différence entre la pseudo-période et 2p/wo qui est la période propre?"
Réponse: on peut le faire ... cliquez si vous n'avez pas peur !
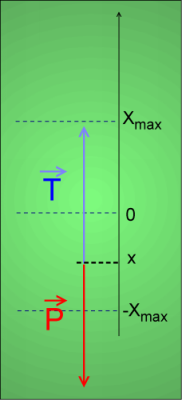
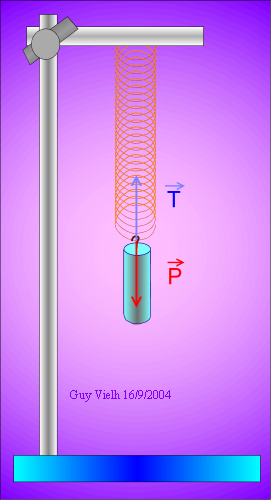
Résumé de l'épisode précédent: Dans le référentiel du laboratoire (suffisamment galiléen pour cette application). Lorsque le crochet qui nous sert d'index est à la position x, deux forces antagonistes s'exercent sur lui.
(nous avons choisi le système: le crochet)
La relation fondamentale de la dynamique dit que la somme des vecteurs
forces extérieures= masse du système x vecteur accélération
le vecteur i est le vecteur unitaire orientant l'axe vers le haut.
Nous projetons cette relation sur la verticale orientée vers le haut:
m.g - k.x - m.g = m. x"
On fait le ménage et il reste:
