
réseau de diffraction gravé sur verre ou sa réplique sur plastique.
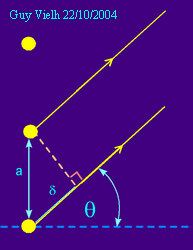
d = a.sin(q).
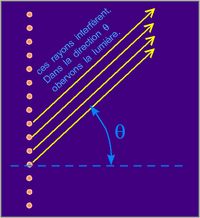
Lorsque d a une valeur quelconque, le déphasage donné par deux fils consécutifs(1 et 2) n'est pas le même que celui donné par les fils(1 et 3) aussi, la somme vectorielle de toutes les contributions est très petite.
Lorsque d est un multiple entier de la longueur d'onde, les interférences sont constructives car ce décalage est le même pour tous les autres fils du réseau. Dans la direction q, toutes les contributions de tous les fils du réseau s'ajoutent.
On a donc de la lumière si :
sin(q) = k.l.
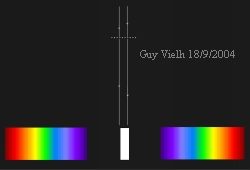
Pour le premier spectre à droite et le premier spectre à gauche k = 1. Ce sont les spectres du premier ordre, ce sont ces deux la qui sont les plus visibles. Comme la lumière rouge a une longueur d'onde plus grande que la lumière violette, la déviation est plus importante pour le rouge que pour le violet. C'est pour cela que le rouge est à l'extérieur des spectres produits par les réseaux.
Pour faire un spectroscope, il faut isoler la source observée et empêcher la lumière de provenir de partout: on enferme ce réseau dans une boîte opaque ... mais voyez donc le spectroscope.