On obtient donc une pulsation w plus petite que la pulsation libre.
Rangeons un peu tout cela:
q" + (r/L)q' + (1/LC)q' = 0 voici la nouvelle équation différentielle.
Pour mémoire, sans résistance, on avait:
q" + (1/L.C)q = 0.
. ..
On obtient donc une pulsation w plus petite que la pulsation libre.
A quoi va ressembler la solution? cela oscille encore à la pulsation w. Mais il y a diminution de l'amplitude avec le temps.
On va essayer une expression q = qmax. e-lt . sin (wt+f)
qmax est la charge du condensateur au départ, on choisit l'origine au moment où referme le circuit, la valeur de f est de +p/2. "l" est la constante d'amortissement dont le calcul nous indiquera la relation avec "r" et "L".
q' = -l .qmax.e-lt . sin (wt+f) + w. qmax. e-lt . cos (wt+f)
q' = -l . q + w. qmax. e-lt . cos (wt+f)
q" = l² . q - l .w. qmax. e-lt . cos (wt+f) - l .w. qmax. e-lt . cos (wt+f) - . . . . w² . qmax. e-lt . sin (wt+f)
q" = q( -w² + l²) - 2 . l . w . qmax. e-lt . cos (wt+f)
l'équation différentielle donne donc en reportant q' et q" de l'hypothèse:
q.[l² - w² + 1/LC - r.l/L] + w . qmax. e-lt . cos (wt+f).[ r/L - 2.l] = 0
Comme x est un sin et l'autre partie un cos, pour obtenir la nullité à tout instant, il faut que la quantité verte et la quantité bleue soient nulles.
l = r/2L et w² =1/LC - r²/4L² = w²o - r²/4L²
Qu'est ce qui change par rapport à un amortissement nul ? Les oscillations existent et elles se tassent exponentiellement. Comme les oscillations mécaniques du pendule vertical.
Lors de la décharge E = 0 ; ou lors de la charge du condensateur.
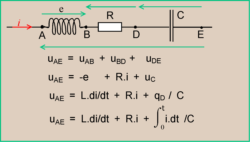
L'intégrale est gênante pour l'exercice de virtuosité que l'on va pratiquer. Nous convertissons tout en charge "q" pour l'armature "D".
di/dt = d²q/dt² = q" .
i = dq/dt . et enfin l'intégrale de i.dt = q
