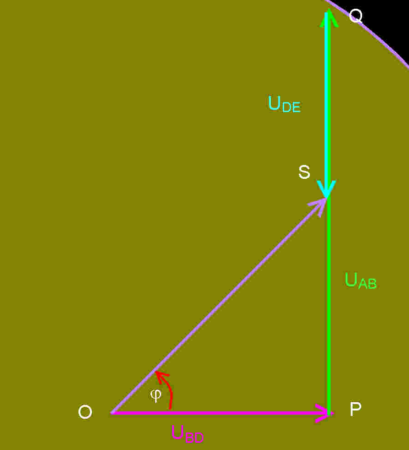
En vecteurs OS = OP + PQ + QS , en projection sur l'axe horizontal alors que la figure tourne : UAE =UBD+ UAB + UDE
uDE = Im/(C.w). cos( wt - p/2 )
en effet, d(cos( wt - p/2 ))/dt =
w.sin ( wt - p/2 ) = w.cos wt.
Y'a qu'à faire la somme des trois u, ils ont la même pulsation. La figure entière tourne autour de O sans se déformer.
Tout se passe comme si on observait la projection sur l'axe horizontal de la somme des trois vecteurs, dessinés sur un disque tournant à la pulsation w .
OS = Um. La projection de OS sur l'axe horizontal, lorsque le disque tourne donne UAE= OS.cos (wt + j ).
Sur la construction de Fresnel, on peut mesurer j . Ou bien se taper les calculs suivants :
tan j = (Lw - 1/Cw) / R
cos j = R / {R²+(Lw-1/(Cw))²}½
Z = {R²+(Lw-1/(Cw))²}½
Um = Z.Im
Um = se mesure à l'échelle sur la consruction de FRESNEL

En vecteurs OS = OP + PQ + QS , en projection sur l'axe horizontal alors que la figure tourne : UAE =UBD+ UAB + UDE
Si nous forçons, avec un générateur, la tension des bornes A et E à être de la forme:
uAE = Um.cos(wt +j )
i est la même dans tout le dipôle parceque c'est une série.
i = Im. cos(wt) regardons chaque terme de la somme des tension:
uAB = L.di/dt = -L.w.Im.sin( wt )
uAB = L.w.Im.cos( wt + p/2 )
uBD = R.Im.cos( wt )