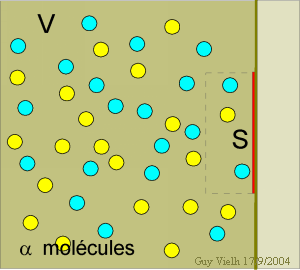
Il faut faire appel à la statistique à cause du nombre gigantesque "a".
Tout comme dans une population les individus n'ont pas tous la taille moyenne, les molécules n'ont pas la même vitesse. Mais nous faisons comme si c'était le cas.
La mécanique nous apprend qu'un objet de masse m et qui se déplace à la vitesse vi
possède une énergie cinétique:
Ei = 0,5 . m . vi². .
L'énergie contenue dans les a molécules de ce gaz parfait est la somme des énergies cinétiques:
E = 0,5. m . a . <v²>
<v²> est la moyenne des carrés des vitesses des molécules. E est l'énergie
interne de ce gaz parfait. On montre expérimentalement et théoriquement que l'énergie
E = 1,5 . T pour une mole de gaz.
Rapporté à une molécule:
m . <v²> = 3 . k . T
(k = constante de Boltzmann )
Un exemple de gaz parfait: il manque la représentation de la dimension perpendiculaire à l'écran. Il manque aussi la prodigieuse agitation des molécules qui se heurtent, rebondissant et frappant les parois. Ceci est montré par l'appareil de simulation: modèle moléculaire des gaz.
On considère que le gaz parfait contient des molécules sphériques rigides et sans autre interactions entre elles que les chocs.
En utilisant ce modèle simplifié, peut-on, en utilisant les lois de la mécanique de Newton au niveau nanoscopique, établir les lois expérimentales macroscopiques des gaz?
La loi du gaz parfait est-elle une conséquence des lois de la mécanique qui régissent les mouvements des objets macroscopiques?
Qu'est ce que la température ? la pression ?
Qu'est ce que l'énergie interne d'un gaz?
Rappelons les hypothèses du gaz parfait.
Un gaz pur parfait est formé d'un nombre a de molécules, toutes pareilles. On peut repérer chaque molécule en la numérotant avec l'indice "i" . La molécule "i" est animée du vecteur vitesse vi . Les molécules occupent un espace de (sont contenues dans le) volume "V".
