A) Quelle relation permet de trouver la vitesse d'un objet dans le référentiel bleu ("immobile").
Cet objet est dans un référentiel vert qui se déplace à la vitesse u dans le référentiel bleu. L'objet est animé d'une vitesse v dans le référentiel vert.
on lance une balle dans un train qui roule et on veut sa vitesse / sol !
B) Dans la physique de Galilée Newton, on ajoute les vecteurs mais cela peut conduire à un résultat scandaleux car rien n'empèche la somme des vitesses de dépasser la valeur limite "c". Or nous savons que ce n'est pas possible.
v a trois composantes : vx' , vy' et vz' nous faisons le raisonnement pour vx'. Il faut faire la même démarche pour vy' et vz' et reconstruire v'
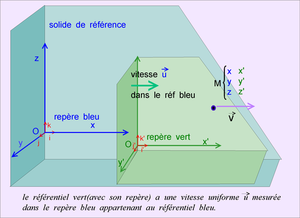
Nous choisissons les axes du repère bleu de manière à ce que la u est selon l'axe ox. Cela simplifie le raisonnement et ne diminue en rien la généralité du résultat.
D) vx = (u + vx')/(1+u.vx'/c²)
le teme du numérateur (u + vx') n'est pas une surprise: c'est le terme galiléen : addition des vitesses mais il est corrigé par le dénominateur: (1+u.vx'/c²) .
Pour vy : vy = y/t = vy'.Ö(1-u²/c²)/(1+u.vx'/c²)
Pour vz : vz = z/t = vz'.Ö(1-u²/c²)/(1+u.vx'/c²)
Pour la lumière produite vers l'avant dans un vaiseau spatial lancé à la vitesse u, sa vitesse pour un observateur immobile est:
v = (u+c)/(1+u.c/c²) = c. L'invariance de la vitesse c est une conséquence de la formule de la composition des vitesses en relativité.
C) Dans le référentiel vert: x' = vx'.t' Mais dans le référentiel bleu:
x = (vx' . t' + u.t')/Ö(1-u²/c²)
mais t' est le temps dans le repère vert, il faut le remplacer par t grâce aux formules de Lorentz:
t = t'(1+u.vx'/c²)/Ö(1-u²/c²)
et , par définition: vx=x/t
