A) Quel nom savant !
Il veut dire que, en remplaçant les grandeurs par leurs dimensions (dans la "formule" provenant du raisonnement littéral du problème que nous traitons) nous pouvons savoir si la formule est cohérente.
Dans sa version simplifiée, on fait fonctionner la formule avec les unités dans le calcul.
B) La réussite de cette l'analyse dimensionnelle ne garantit pas que la formule est juste mais qu'elle est possible. Vous avez pu oublier un coefficient sans dimension ...
Mais son échec signale sans ambiguïté que la formule est fausse!
D) c est la circonférence c = p . F
(F est le diamètre de la roue: en m) et f c'est la fréquence de la roue (le nombre de tours par seconde: en s-1)
si la première formule est la bonne on a :
v = p.F.f º m . s-1 cela correspond bien à une vitesse ! la formule est possible.
Par contre la seconde proposition
v = c / f = p . F / f º m . s , là ça ne va pas, cette formule est fausse.
Attention : v = F . f a la bonne dimension ( m.s-1) mais elle est fausse, on a oublié le coefficient sans dimension p .
E) les malins qui ont déjà regardé les questions de rotation ont trouvé la formule:
v = R . w
dans laquelle R est le rayon de la roue et w la vitesse angulaire en rad.s-1 . Ne serait-ce pas la même? Ben oui évidemment !!!
w = 2.p.f puisque 1 tour c'est 2.p rad ...
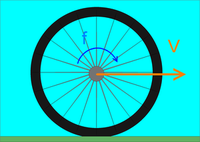
C) Voici un exemple de vérification. La question à résoudre est par exemple de calculer la vitesse de rotation de la roue d'un vélo alors que l'on connaît la vitesse du vélo.
On sent bien que la circonférence "c" de la roue joue un rôle dans cette histoire. Il y a proportionnalité. Mais vous ne vous souvenez plus laquelle:
v = c x f ou bien v = c / f ???
