Tiens, cela n'est pas exactement la même formule que lorsque c'est le récepteur qui se déplace? C'est une histoire que résout la relativité d'Einstein. Il faut que l'expression soit la même dans les deux situations.
soit : d = -c.t + SoA + vr.To + c.To
Cette onde frappe le récepteur à la date t2
t2 = ( SoA + vr.To + lo)/c
or t2 - t1 = T (période apparente)
T = vr.To/c + lo/c ou encore
l = lo. vr/c + lo
vr/c = (l-lo)/lo
Tiens, cela n'est pas exactement la même formule que lorsque c'est le récepteur qui se déplace? C'est une histoire que résout la relativité d'Einstein. Il faut que l'expression soit la même dans les deux situations.
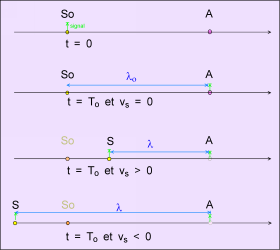
Considérons cette fois le cas où la source se déplace dans le référentiel du récepteur: par exemple la voiture des pompiers fonce vers nous ou bien s'en éloigne. L'air qui est le milieu matériel dans lequel le son se propage est immobile pour nous. La vitesse du son est donnée dans le référentiel de l'air et donc aussi du récepteur.
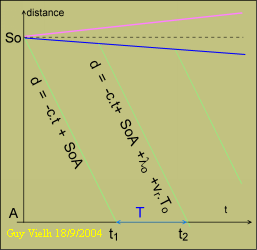
A la date t = 0 la première onde est émise par la source. Ce front atteint le récepteur en t1. Les équations horaires sont sur la figure à fond kaki. t1 = SoA/c
La deuxième onde est émise par la source à la date To. Mais la source a bougé: elle se trouve à d = SoA + vr.To.
Cela conduit à une équation horaire pour le deuxième signal: d = -c.t + b avec
SoA + vr.To = -c.To + b