Pour calculer J, on somme le produit de chaque masse
élémentaire du solide en rotation par le carré de sa
distance à l'axe.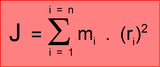
En résumé:
MF/D = d . F . sin(a) . cos(b)
Le signe est donné par la règle du "tire bouchon" sur le schéma, F ferait avancer le tire bouchon vers le haut: MF/D > 0
Pour calculer J, on somme le produit de chaque masse
élémentaire du solide en rotation par le carré de sa
distance à l'axe.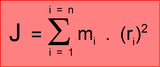
Le théorème des moments permet de traiter les objets tournant dans les équilibres et la dynamique de leurs mouvements.

Lorsque plusieurs forces s'exercent sur l'objet pouvant tourner autour de l'axe D: on additionne les moments des différentes forces par rapport à cet axe. Dans un référentiel galiléen, dans un repère centré sur l'axe de rotation,
L'accélération angulaire a" = (somme des M)/ J ........ J = moment d'inertie .
Le moment de la force F par rapport à l'axe D donne l'effet que va avoir cette force F pour la rotation qui se fera en utilisant cet axe.
Si l'angle a vaut 0 ou 180°, la force ne contribuera pas à la rotation. La formule donnant le moment contiendra "sin(a)"
Si l'angle b est de 90° ou de 270° la force F n'aura aucun effet. La formule donnant le moment contiendra "cos(b)"
Il est évident que F aura le maximum d'effet si elle est dans le plan beige et si elle est perpendiculaire au bras de levier "d" : sin(a) = 1, cos(b) = 1
Le moment est un vecteur axial obtenu par l'opération:
MF/D = d ^ F'
les trois termes sont des vecteurs. L'opération notée "^" est le produit vectoriel. La grandeur du vecteur F' est F.cos(b)