Il y a donc les mêmes solutions et les mêmes réactions aux paramètres y compris si il y a de l'amortissement.
Projetons cette relation sur l'axe horizontal et sur l'axe vertical pour pouvoir traiter le problème:
Sur l'axe vertical, SI LE RAIL SOUFFLANT EST HORIZONTAL: P = R et il n'y a aucun mouvement selon cet axe. Circulez, rien à voir!!!
Sur l'axe horizontal (l'arrête du rail par exemple). On a - 2.k . x = m x"
Exactement la même équation différentielle que pour le pendule vertical au coeff 2 près (parce qu'il y a deux ressorts) mais cela ne changera pas le type des solutions !!!
Il y a donc les mêmes solutions et les mêmes réactions aux paramètres y compris si il y a de l'amortissement.
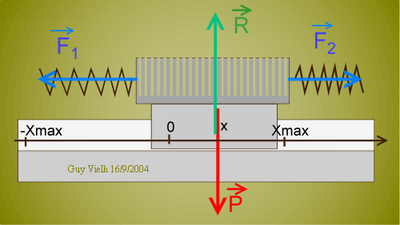
F1 = k . (x + xo) ;.... F2 = k . ( -x + xo) . ;. xo = position dont sont étirés les ressorts en position de repos. La somme des deux forces bleues: - 2.k.xo les deux ressorts se comportent comme un seul ressort de raideur double.
Sur la figure de droite on voit que l'on fait bien de choisit l'origine des x au point d'équilibre du système des deux ressorts .
On étire le ressort jusqu'à la position -Xmax et on le lache sans vitesse initiale.
En tout point X quelconque, quatre forces s'exercent sur le mobile autoporteur. En bleu, la traction des ressorts, en rouge le poids du cylindre. En vert la force pressante du coussin d'air.
Une loi relie les quatre forces à l'accélération du mobile:
C'est la relation fondamentale de la dynamique: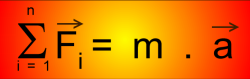
Nous choisissons le référentiel terrestre.
