en choisissant le passage de gauche à droite à l'origine des x comme origine des dates.
Si il y a amortissement ? soit f le coeff de frottement, il faut ajouter une nouvelle force proportionnelle à la vitesse et opposée à elle ( -fx') dans la relation fondamentale de la dynamique:
-2.k.x - f.x' = m.x"
qui admet comme solution:
x = Xmax. e-(f/2m).sin (wt + f)
avec w² = wo² - l² et l = f/(2m)
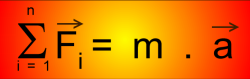Sur
l'axe horizontal (l'arrête du rail par exemple) On a
- 2.k . x = m x"
k étant la raideur d'un seul ressort et on a pris les deux ressorts identiques. Si ils ne sont pas de même raideur: k1 + k2 remplacera 2k.
Pourquoi faire simple quand on peut faire compliqué?
Les solutions ? Toujours pareil!
x = Xmax. sin (wot + f)
x' = wo . Xmax . cos (wot + f)
x" = -wo2 .Xmax .sin (wot + f) = -wo²x
wo² = 2.k/m et f = 0
