Dans le cas d'un solide quelconque formé de n morceaux de masse mi distants de ri au centre de rotation
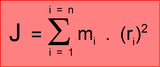
J est le moment d'inertie du corps.
moment du couple = S m.R².a".s
L'accélération angulaire a" est constante (c'est un solide), on la met en facteur:
moment du couple = a".s . S (m.R²).
On définit:(somme des m.R²) = moment d'inertie par rapport à l'axe (noté J, en kg.m²)
Dans le cas d'un solide quelconque formé de n morceaux de masse mi distants de ri au centre de rotation
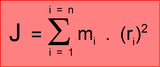
J est le moment d'inertie du corps.
La relation fondamentale de la dynamique des corps en rotation est :
S(MF/axe) = J.a".s
.
1
.... .... .... .... .... ..2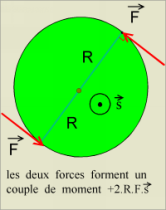 
. .. . . ............... . .3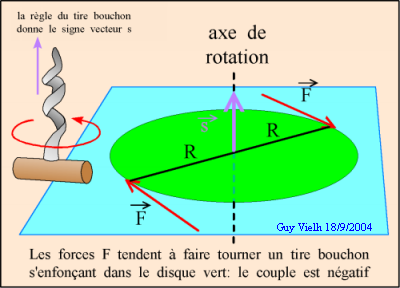 
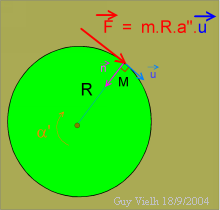
Considérons le cas où il n'y a qu'un point matériel, une force F qui suit ce point. La relation fondamentale de la dynamique dit que:
F = m . a rappelons nous que les écritures rouges sont des vecteurs. Si nous voulons faire apparaître le moment de la force F, multiplions par R des deux côtés de cette égalité:
F.R = m .R. a = m.R.R.a" C'est la situation de la figure 1. Le moment de F (nous le noterons: MF/axe) est négatif.
Organisons cette écriture :
MF/axe = m.R².a".s (I)
Dans le cas où nous avons un solide en rotation, le couple contient deux forces: leur somme est nulle mais elles ont un moment
S(MF/axe) = 2.F.R. s . dans le cas de la figure 2 il est positif.
Le solide est constitué d'un ensemble de points dont chacun obéit à la relation (I)
