Voyons maintenant le cas plus concrêt d'un solide soumis à un couple de forces:
.
C'est la situation de la figure 1. Le moment de F (nous le noterons: MF/axe) est négatif.
Organisons cette écriture en incorporant le signe dans a":
MF/axe = m.R².a".s (I)
Dans le cas de la figure 1 nous obtenons une accélération négative selon l'orientation choisie pour "s":
Si le point M tourne dans le sens rétrogade, (négatif) il va tourner dans ce sens rétrograde encore plus vite après l'action de F.
Si il tourne dans le sens positif, l'action de F va faire diminuer cette vitesse. (accélération angulaire négative).
Voyons maintenant le cas plus concrêt d'un solide soumis à un couple de forces:
.
fig1 /.2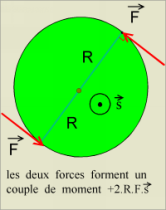 
. .. . . .
Considérons le cas où il n'y a qu'un point matériel, une force F qui agit sur ce point. La relation fondamentale de la dynamique dit que:
F = m . a
rappelons nous que les écritures rouges sont des vecteurs.
Nous voulons faire apparaître le moment de la force F, car l'expérience nous apprend que le moment de la force est le facteur important dans cette histoire.
Multiplions vectoriellement par R.n des deux côtés de cette égalité:
FÙR.n = m .R. n Ù n = - m . R .|| a || . s
= - m.R.R.|a"| . s
Le signe négatif est dù à ce que le produit vectoriel de la figure 1 donne un vecteur qui s'enfonce dans le dessin. Opposé à s . (Le tire bouchon s'enfonce dans le dessin si on le tourne selon F)
