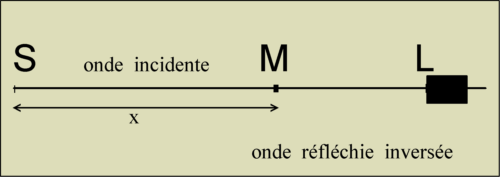
YiM = A.sin [ 2.p.f.(t - x/v)]
Mais cette onde lorsqu'elle arrive sur l'obstacle se réfléchit en s'inversant (apparition du signe "-") et parvient aussi en M mais avec un retard dt' = distance parcourue/v : dt' = (2L-x)/v
YrM = - A.sin [ 2.p.f.( t - (2L-x) / v ) ]
............. ......
En M l'onde incidente et l'onde réfléchie s'ajoutent: YM
=YiM +YrM
YM = A.sin [ 2.p.f.(t - x/v)] - A.sin [ 2.p.f.( t - (2L-x) / v ) ]
Nous cherchons les valeurs de x pour lesquelles YM = 0 quelle que soit la valeur de t (après que le système d'onde se soit établi ) : Ces points d'amplitude continuellement nulle sont les noeuds de vibration.
2.p.f.(t - x/v) = 2.k.p + 2.p.f.( t - (2L-x) / v ) on divise par 2.p.f
t - x/v = k/f + t - (2L-x) / v ; on simplifie puis multiplie par v
2L - 2x = k.v/f = k.l ou encore L - x = k . l/2.
or L = n.l /2, par conséquent x = (n-k)l/2 , les noeuds sont espacés de l/2 , il y en a un en S (x=0 lorsque n = k) et un autre en L (lorsque x =L = nl/2 :k = 0 car il ny a aucun décalage temporel en L)
Nous sommes dans le cas d'une corde tendue entre S et L. Les deux extrémités sont inverseuses. L'onde partant de S s'inverse en heurtant L et s'inverse de nouveau en heurtant S. Elle revient identique à celle donnée par S. Si on admet que le système est stationnaire, cela veut dire que l'ancienne onde et la nouvelle doivent se superposer exactement.
Il faut donc que le temps mis par l'ancienne onde pour parcourir l'aller+retour (2L/v) soit un multiple de la période T ; donc 2L/v = n.T
L = n . vT/2 = n . l/2 Il n'y a d'ondes stationnaires que si L est un multiple de la demi longueur d'onde
L'onde émise en S a comme amplitude YS, prenons le cas d'une onde sinusoïdale: YS = A.sin [ 2.p.f.t ]
cette onde arrive en M avec un retard dt = x/v. Ainsi, l'amplitude de l'onde provenant de S qui arrive en M a comme expression:
