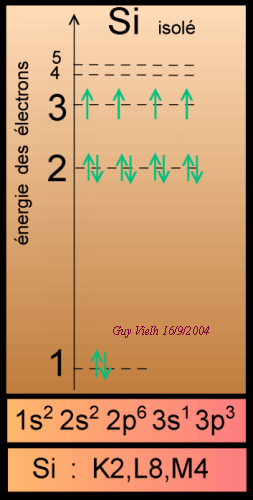
On voit le dernier niveau occupé, c'est le niveau n=3. On l'appelle aussi la couche M. Il est tétravalent car il peut accepter 4 électrons ou prêter 4 électrons de cette couche pour atteindre la règle de l'octet.
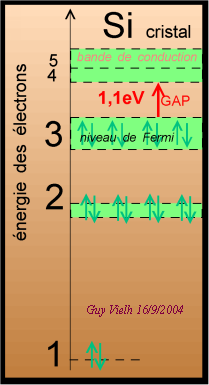
Dans un monocristal de silicium, cet atome a des voisins proches.
Cette proximité va créer un grand nombre de sous de sous-niveaux par effet LCAO.
Les niveaux vont se "marcher dessus" pour donner des "bandes". C'est le niveau 3 qui sera le plus affecté puisque c'est le niveau de valence. Conformément à la LCAO, l'énergie de ces niveau est plus basse, 4 liaisons par atome vont s'établir et on obtient le diagramme de droite.
Ceci transparaît dans les spectres d'absorption de la lumière.
Les niveaux supérieurs, 4,5,6 ... sont élargis au point de se
recouvrir. Si un électron va dans la bande de conduction, il peut se
déplacer dans tout le cristal qui sera alors conducteur de l'électricité.
Pour cela, il faut fournir au moins 1,1 eV à un électron du
niveau de Fermi. La chaleur, la lumière
peuvent faire cela. Mais à froid, sans rayonnement, Si est un
isolant.
Le niveau le plus élevé qui contient des électrons, dans
l'état fondamental, est le niveau de FERMI.
Un atome isolé (c'est à dire loin de tout autre atome, sans champ magnétique, électrique, sans lumière violente, pas trop chaud....) finit par se trouver dans l'état fondamental = l'état d'énergie minimale.
Chaque électron occupe alors une place (dans les niveaux d'énergie donnés par l'équation de
Schrödinger) telle que l'énergie totale est la plus petite possible.
Les niveaux d'énergie sont très fins et parfaitement définis. Sur l'image, pour simplifier, on a considéré que les niveaux sont simples. Mais les nombres quantiques l et m donnent une structure "hyperfine" qui
apparaît dans le notation complète de la structure électronique (L se divise en 2s et 2p). Nous nous intéressons à l'énergie et pas à la forme spatiale de ces orbitales.
Faisons un diagramme d'énergie pour un atome de Si (silicium) isolé (dans son état fondamental). A gauche.
